Predeterminación del tamaño de la muestra para estimar un parámetro poblacional: Media o proporción
Resumen
Una vez hemos definido la población que queremos estudiar (población de estudio, experimental o de referencia), el siguiente paso es determinar el número de sujetos que queremos estudiar, es decir el tamaño de la muestra, lo cual va a tener una gran importancia ya que en ocasiones puede condicionar la viabilidad del estudio. La predeterminación del tamaño de muestra es una tarea que se debe realiza durante la fase de diseño de un estudio, es decir, debe decidirse antes de la ejecución del estudio.
Los aspectos susceptibles de ser considerados para efectuar este cálculo son amplios y variados, y la elección concreta que se haga depende, entre otras cosas, del objetivo y tipo de diseño, descriptivo o analítico, es decir, si nuestro objetivos es estimar un parámetro población o contrastar una hipótesis. También depende del tipo de variable, cuantitativa, o cualitativa.
Por ejemplo, en un estudio transversal para estimar la prevalencia de HTA en una población, se requerirá un tamaño de muestra que permita estimar dicha prevalencia con una determinada precisión. En cambio, en un ensayo clínico de un nuevo fármaco comparado con un placebo, el tamaño de muestra debe permitir detectar, por ejemplo, con una determinada potencia, una reducción del riesgo de mortalidad después de un año de seguimiento. En el primer caso, el objetivo es la estimación de un parámetro; en el segundo se trata de contrastar una hipótesis pretende analizar si hay un efecto estadísticamente significativo de un tratamiento. En cada uno de estos dos contextos, estimación o realización de pruebas de hipótesis, se abren a su vez diversas posibilidades.
En esta unidad vamos a centrarnos en la predeterminación del tamaño de la muestra para estimar un parámetro poblacional: media o proporción.
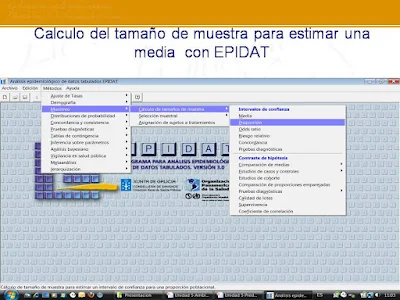
Calculo del tamaño muestral para estimar una media
En esta situación, el tamaño de la muestra está determinado por varios factores:
- La precisión de la estimación, que se mide a través del error muestral. La magnitud del máximo margen de error admisible debe ser fijada por el investigador, pues es él quien mejor identifica las consecuencias prácticas de un error dado. Si, por ejemplo, lo que se quiere es conocer la media del colesterol de una población y se admite un error de hasta 50mg/dl, ello significa que el valor de la media que obtengamos podrá tener una variación de +_ 50mg/dl. En general se cumple que al aumentar la precisión, es decir, al disminuir el grado de error, aumenta el tamaño de muestra necesario, lo que coincide con el sentido común. Epidat permite calcular tamaños de muestra para distintos valores de precisión y proporcionando el tamaño de muestra correspondiente a cada uno de esos valores.
- El nivel de confianza, que generalmente se fija en 95%. El efecto de este valor sobre el tamaño de muestra es directo; es decir, para una precisión dada, el tamaño de muestra aumenta al aumentar el nivel de confianza.
- La varianza o la desviación estándar de la población. Este valor tendremos que obtenerlo a partir de estudios previos o de un estudio piloto.
- Tamaño de la población. En la mayoría de las situaciones nos va a resultar difícil conocer el verdadero tamaño de la población de la que procede la muestra. Pero esta circunstancia tiene escasa influencia sobre el tamaño de la muestra si trabajamos con poblaciones grades, mas de más de 5.000 elementos. En caso obtener una muestra de una población pequeñas, si nos interesa conocer el marco muestral , ya que el tamaño de la muestra que predeterminamos será algo menor que si consideramos la población como infinita.
Calculo del tamaño muestral para estimar una proporción
En esta situación, el tamaño de la muestra está determinado por los siguientes factores:
- La precisión de la estimación. La magnitud del máximo margen de error admisible debe ser fijada por el investigador, pero a diferencia del cálculo para una variable cuantitativa la precisión absoluta será dada por un % . Si, por ejemplo, lo que se quiere es conocer la prevalencia de HTA de una población y se admite un error de hasta 5%, ello significa que el valor de la prevalencia que obtengamos podrá tener una variación de +_ 5%. Como en el caso de la media, se cumple que al aumentar la precisión, es decir, al disminuir el grado de error, aumenta el tamaño de muestra necesario. En este casos también Epidat permite calcular tamaños de muestra para distintos valores de precisión, proporcionando el tamaño de muestra correspondiente a cada uno de esos valores.
- El nivel de confianza, que generalmente se fija en 95%. El efecto de este valor sobre el tamaño de muestra es directo; es decir, para una precisión dada, el tamaño de muestra aumenta al aumentar el nivel de confianza.
- La proporción esperada. Este valor tendremos que obtenerlo a partir de estudios previos o de un estudio piloto. Es muy habitual encontrar en manuales y artículos la recomendación de utilizar el valor del 50%, cuando no se conoce en absoluto el valor de la proporción P, esta es una decisión basada en el argumento de que dicho valor es la situación mas desfavorable, en la que es requeido el máximo tamaño de muestra para cualquier valor de la proporción P.
- Tamaño de la población. El efecto es similar al comentado previamente para una media .















Comentarios
Publicar un comentario
Este es un blog dirigido a profesionales sanitarios. Los comentarios están sujetos a moderación por el autor antes de su publicación, no admitiéndose publicidad, comentarios no profesionales, no fundamentados científicamente, ni aquellos que resulte inapropiados u ofensivos, etc. Tampoco, en ningún caso a través del blog o correo electrónico, se atenderán casos clínicos particulares ni se dará información personalizada. Si algún paciente desea ser atendido en consulta puede solicitar cita en el teléfono indicado para tal fin.